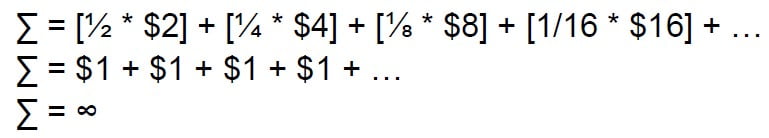Farnam Street Investments commentary for the month of January 2021, discussing non-ergodicity and investing.
Q4 2020 hedge fund letters, conferences and more
Lottery Paradoxes
The poorest third of Americans buy more than half of the lottery tickets. By now, everyone knows buying a ticket is a negative expected outcome bet. The odds multiplied by the payout are a losing proposition. Is the lotto nothing more than a predatory tax on the poor and ignorant?
I used to think so, but the truth may be more nuanced than I understood. As we explore why, we’ll meet an 18th-century mathematician whose work explained how an airplane wing generates lift. We’ll also meet a 19th-century physicist who provided a statistical explanation for the second law of thermodynamics and has a constant named after him related to the temperature of gases. We might even learn a few new terms.
Lastly, we’ll tie everything together to explain why there’s more than one flavor of “average” and what it means for your investments and safe rates of withdrawal for a portfolio.
To start, let’s play a simple game...
I put $2 into the pot and toss a fair coin. If it’s heads, I’ll double the pot and we’ll keep playing. If it’s tails, the game is over and you get what’s in the pot. So if a tails comes up after one heads, you get $4. After two heads, you get $8. After three heads, $16. If you were lucky and got 10 heads in a row, you’d win $1,024. Simple enough.
First important question: what’s the average expected payout?
I’ll give you an assist with the math:
x = 2k where k = the number of tosses. You have a 50% chance at $2, 25% chance of $4, ~12% chance of $8, ~6% chance of $16, etc. When we sum those up, we get:
The mathematical expected payout is infinity. Oddly dissatisfying, as it feels like we’d get a tails relatively soon and we’d be nowhere near infinity.
Next important question: how much would you pay to play this game? With an expected payout of infinity, the logical answer is there’s no price too high. A billionaire should be willing to pledge every cent she has to play a game with an infinite expected outcome.
Yet that doesn’t fit our intuition. Would you sacrifice your entire net worth to play this game where you know a tails could happen on the next flip, and your gut says you probably couldn’t buy dinner with your likely result?
This thought experiment was first proposed in 1738 by a Swiss mathematician named Daniel Bernoulli.2 His work in fluid dynamics eventually led to the naming of the Bernoulli Principle, which explains how the wings of an aircraft provide lift due to pressure differentials. Bernoulli was living in St. Petersburg, Russia at the time, hence this infinite expected value phenomena is called “The St. Petersburg Paradox.”
In 1957, a researcher at MIT named David Durand published an article called “Growth Stocks and the Petersburg Paradox.” Durand observed that many high growth companies exhibit exceptionally high payoffs, similar to the St. Petersburg Paradox. A small minority of them will be the equivalent of getting 40 heads in a row in our game. Given this paradoxical condition, you’d expect market participants to misprice this optionality at times and pay too much for growth. It was a mystery how to properly value companies with such extreme right-tail outcomes in 1957. Little has been resolved. You can’t help but hear echoes from the past when thinking about the software-as-a-service cloud darlings of today. Some could be tremendous “40-heads winners,” but it’s likely foolish to bet on the cohort at today’s lofty prices. There’s nothing new under the sun.
Back to Bernoulli. He had another insight: all money isn’t created equally. Its holder experiences a diminishing marginal utility. The more you already have, the less the next dollar is worth to you. A billionaire isn’t infinitely wealthy, but there’s only so much money you can spend in your waking hours. As Warren Buffett has said, “Why risk what you have and need for what you don’t have and don’t need?” Bernoulli proposed the idea of “logarithmic utility” to capture this characteristic of diminishing returns.3 In this instance, someone with a net worth of $1 million should be willing to pay up to $20.88 to play our game. A net worth of $1,000 should pledge $10.95. This feels closer to our intuition.
If wealth follows a natural log pattern, someone of modest means is following mathematical logic when playing the lotto, despite the daunting odds and apparent foolishness. I was wrong to sit in quiet judgement of the disadvantaged lotto players.
It’s unpopular to say this in serious investor circles, but I believe the same can be said for the muchmaligned “Robinhood” crowd today. They’re insatiable appetite for risk in buying deeply out-of-the-money call options and affair with leverage could be logical under certain conditions. Given the get-rich-quick feel, I’m skeptical that logarithmic utility functions are dancing through their heads. But who knows? I wish them luck.
Not-Your-Average Average
Did you know there are at least two kinds of averages?
Ludwig Boltzmann was a 19th-century Austrian physicist and philosopher. His greatest achievement was a statistical explanation of the second law of thermodynamics which described macroscopic observations, like temperature and pressure, with microscopic parameters that fluctuate around an average. Today it’s called kinetic theory and it describes the molecular speeds of gases.
Boltzmann was a gifted statistician who coined the obscure term “ergodic.” Some examples will help explain the concept.
I hand you a 6-sided die and ask you to roll it 100 times in a row. You’ll likely get a three around 17 times.4 The “time-series” average of you rolling a die over and over for a few minutes is 17.
If I hand 100 dice to 100 different people and they each rolled it once, we’d expect around 17 of them to also report rolling a three. The so-called “ensemble” average is 17, just like the “time-series.”
When the time-series average and ensemble average are identical, Boltzmann described the situation as “ergodic.” Ergodic systems tend to be admittedly boring. Most human systems are non-ergodic. The time series average can vary greatly compared to the ensemble. And assuming ergodicity of a non-ergodic system can get you killed.
Imagine you find yourself sitting at a table with five other people. There’s a vintage six-shooter loaded with one bullet sitting at the center of the table. You’re instructed by your sadistic captor that you must play Russian Roulette. Each person is required to put the gun to their head and pull the trigger one time. Those who survive will each be released with $10 million. You have a five-in-six chance of coming out ahead, implying an ensemble average expected outcome of $8,333,333. Therapy bills aside, it’s not a bad monetary predicament.
Now, imagine an identical scenario, except you’re the only one sitting at the table. You’re required to pull the trigger six times in a row. Your time-series average outcome drops, along with your odds of survival, to zero. There’s quite the deviation between the ensemble and time-series averages. This is non-ergodicity in the extreme.
Non-Ergodicity and Investing
In the investment world, non-ergodicity leads to blindspots in risk-taking. First, our ability to participate in the next round can depend on the consequences of today’s decisions (see: Russian Roulette). Avoiding zeros of all stripes5 becomes paramount. As Charlie Munger has observed, “It is remarkable how much long-term advantage people like us have gotten by trying to be consistently not stupid, instead of trying to be very intelligent.”
Non-ergodicity helps explain my aversion to all forms of leverage. Margin debt in a portfolio makes you vulnerable to price swings. Nothing needs change at the business level for the price to move and take you out. Corporate debt makes a company vulnerable to the timing of their cash flows. The briefest of mismatches can make your equity worth zero. Naturally, Warren Buffett says it all better than I can: “Over the years, a number of very smart people have learned the hard way that a long string of impressive numbers multiplied by a single zero always equals zero.”
Second, there are infinite possible futures, but only one will be realized. The future is a million strands woven in the present to become the rope of history. We can do everything right and not necessarily get the average expected outcome.
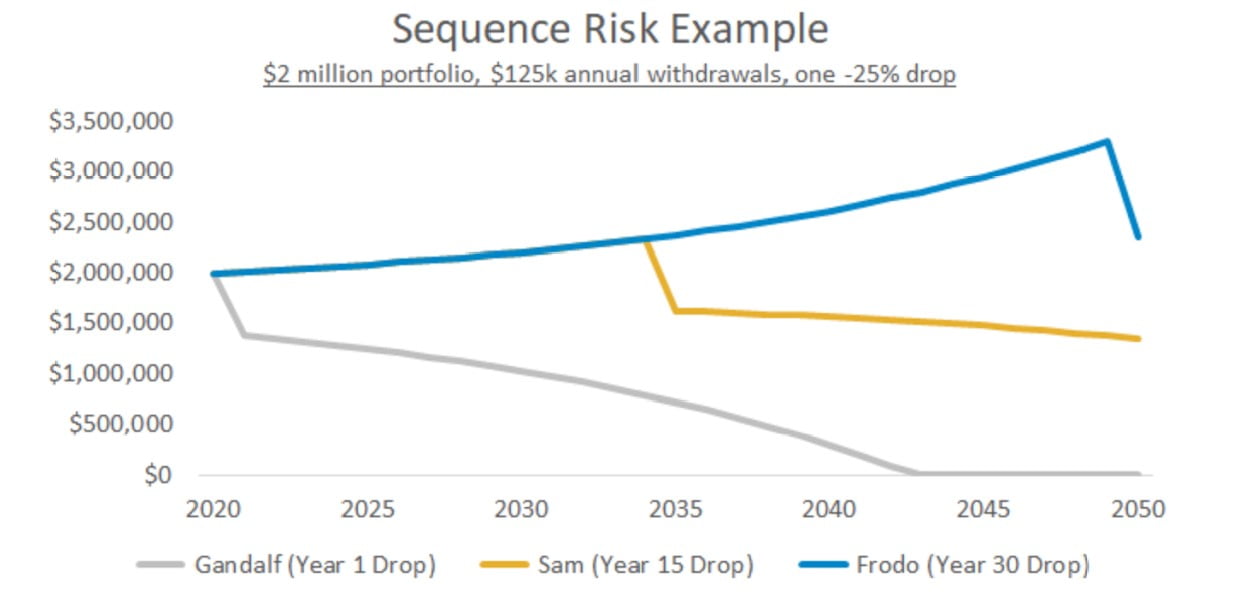
Non-ergodicity has a material impact on safe rates of portfolio withdrawal. Adam Collins of Movement Capital raises an interesting hypothetical using Lord of the Rings characters. Each investor starts with a $2m portfolio, earns an identical 7% return, and withdrawals $125,000 per year.6 The sole difference is the timing of a -25% drop. This is called “sequence risk.”
Gandalf experiences an immediate loss. Sam’s loss comes after 15 years. Frodo’s after 30 years.
As you can see, Gandolf’s early misfortune introduces heavy gravity and his portfolio craters. Frodo has no problem as he achieves escape velocity early--the late loss has a muted effect. All three have identical initial conditions: portfolio size, annual return, withdrawal amount. All we change is the sequence of a pedestrian loss of -25%. Such is the danger lurking in averages and a misunderstanding of non-ergodicity.
Market Update
“In an investment context, the difference between ensemble averages and time averages is often small. It becomes important, however, when risk increases, when correlation hinders diversification, when leverage pumps up fluctuations, when money is made cheap, when capital requirements are relaxed.” -- Ole Peters
Based on Peters’ above description, it sure seems we’re in a time where we could expect ensemble and time averages to part ways. Let’s tackle each of his five above conditions graphically.
-
"When risk increases...”
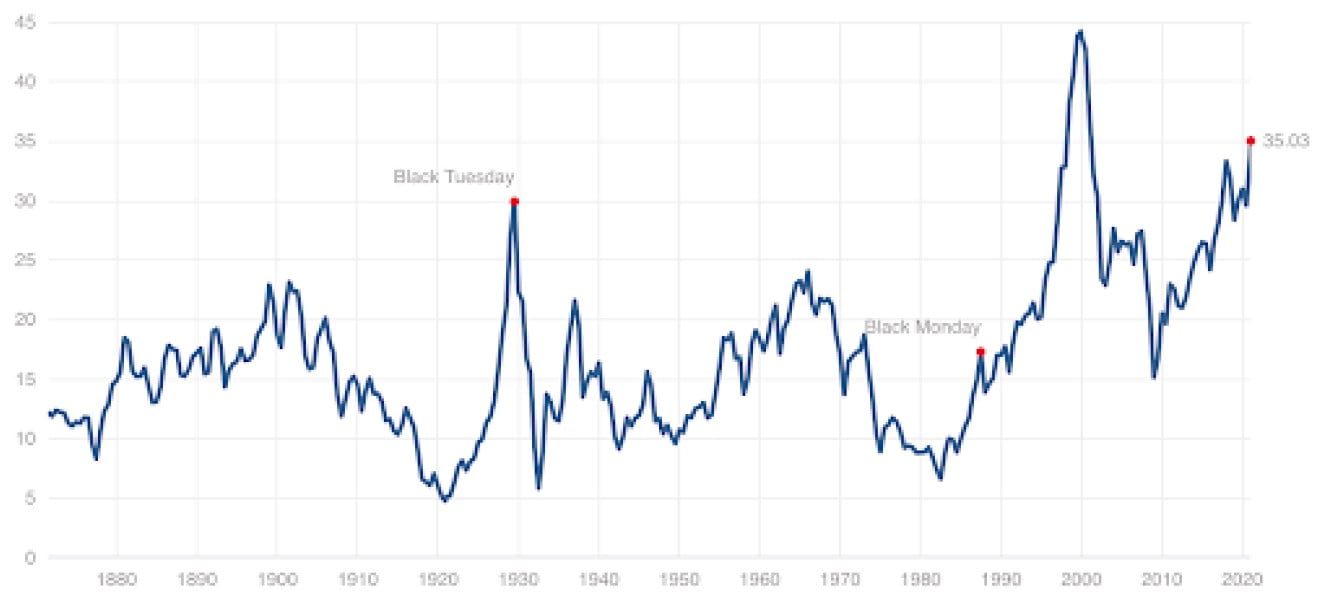
The Shiller CAPE ratio compares the price to the average of the last ten years earnings.7 We’re at 35x, rarified air, only eclipsed by the pinnacle of 44x in 1999. Inevitably, a high starting price for CAPE has been a risky proposition for expected forward returns.
-
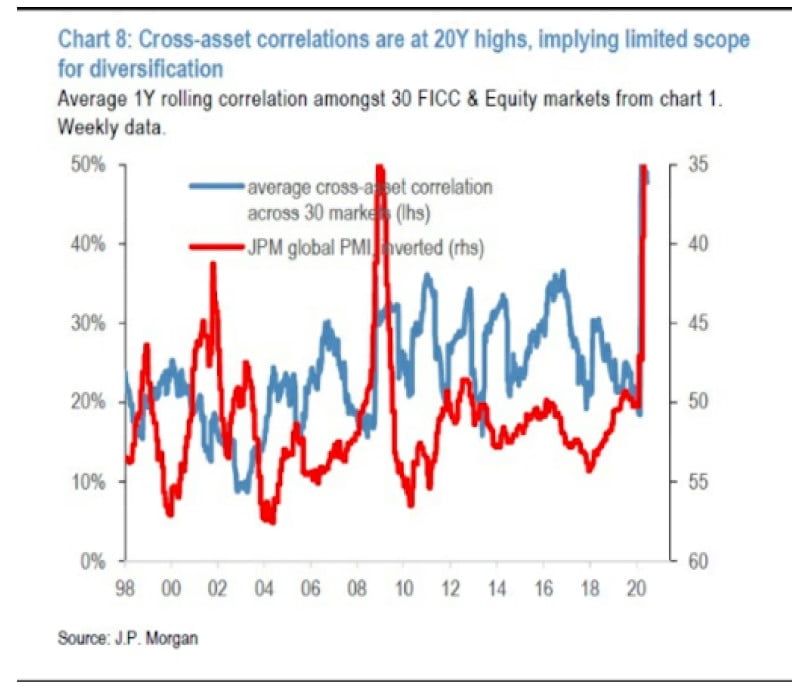
"When correlation hinders diversification...”
When the price of assets are moving together, it’s difficult to reduce risk via diversification.
-
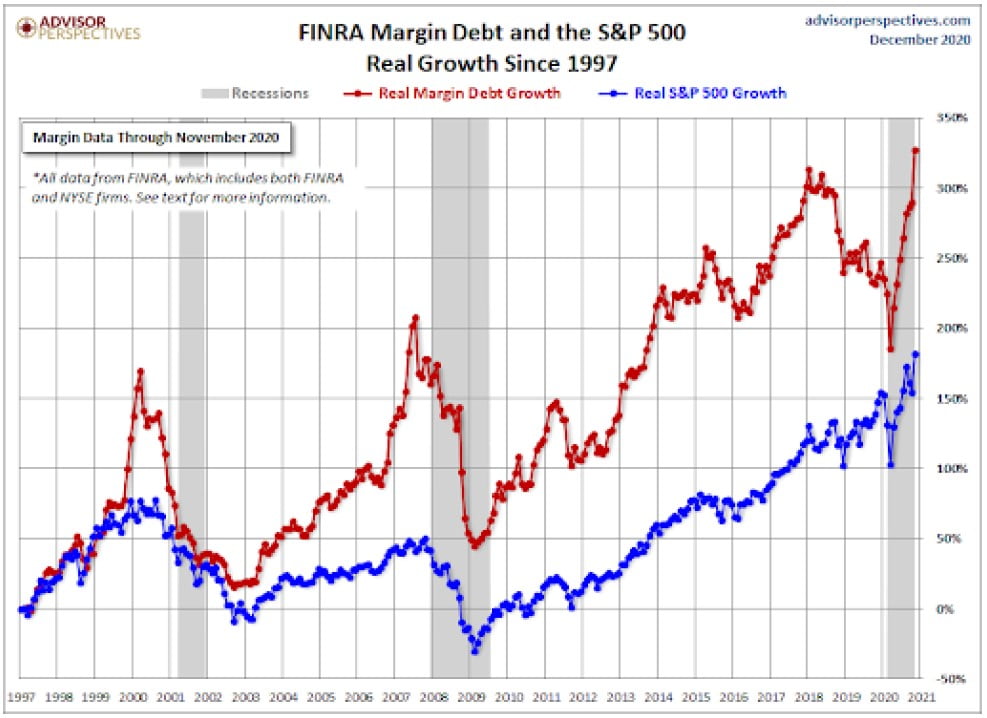
“When leverage pumps up fluctuations…”
Spikes in margin debt tend to occur at market tops. The future looks rosy, so people are willing to borrow now to capture more of the promised future upside. Prices are driven higher by increased buying power, increasing confidence. For a while. “Margin calls” are this process working in reverse.
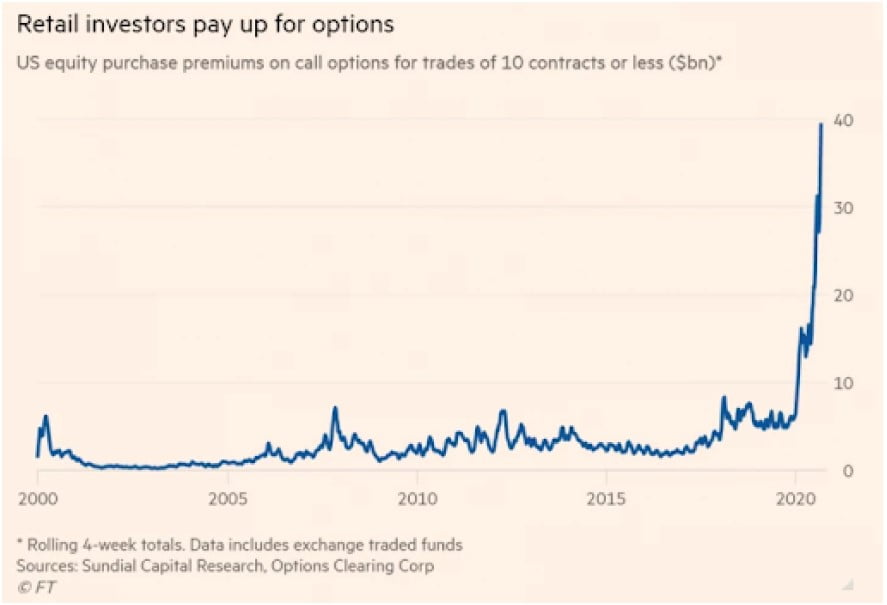
Another way to increase leverage is via options. For a call option, you can pay a small amount upfront. If the stock goes up a lot before your option expires, you can make even more than if you just held the underlying security. If the price only goes up modestly, your investment can go to zero. Options can produce enviable gains in a rapidly rising market, like doubling down on every bet at the casino. But gravity always prevails, and zeroes will catch you flatfooted. Small retail investors have discovered the intoxicating juice out-of-the-money options can provide. This is a very dangerous game to play, even for the sophisticated investor.
-
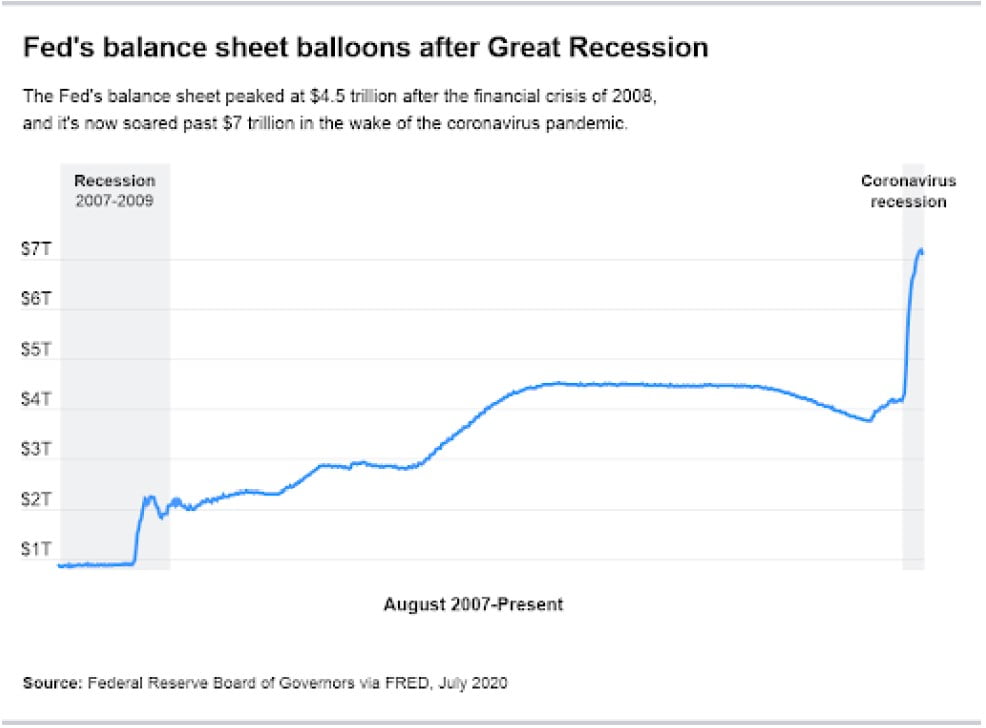
“When the money is made cheap…”
The Federal Reserve’s balance sheet has nearly doubled in the last year. Notice how modest the 2008 policy response appears compared to recent actions. We’re all participants in a grand monetary experiment of cheap money.
-
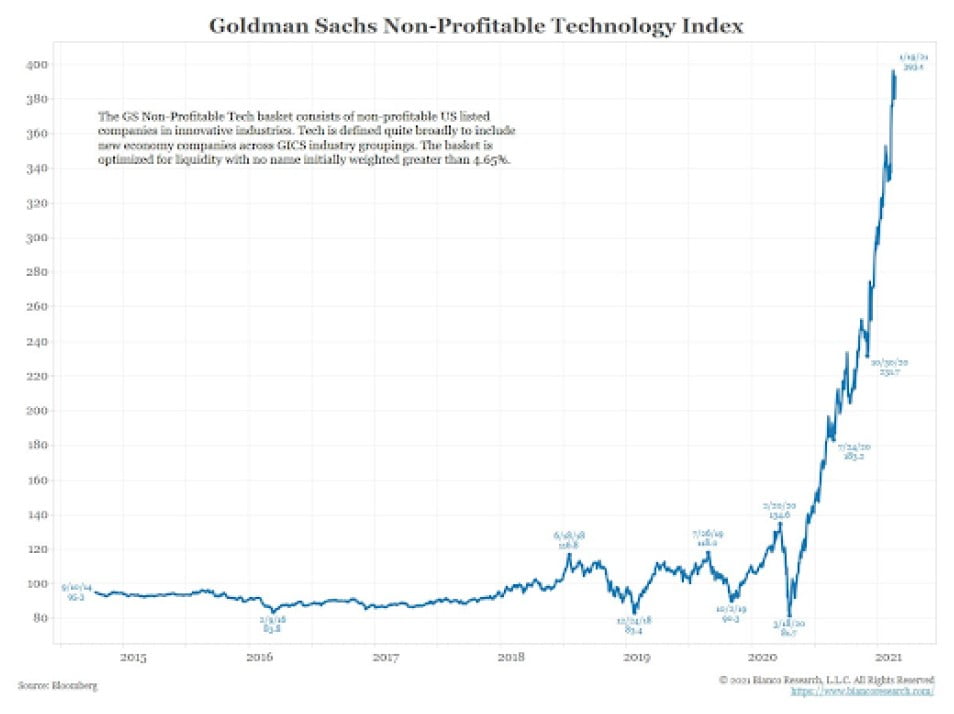
"When capital requirements are relaxed..."
Skepticism is subdued as people have bid up money-losing companies in hopes of a promised future of high-tech dominance.
Takeaway: Caution is advised when dealing with non-ergodic systems. Here be dragons.
As always, we’re thankful to have such great partners in this wealth creation journey.
Jake