By Dr. Atanu Saha – Chairman, Data Science Partners Burton Malkiel – Chemical Bank Chairman’s Professor of Economics, Emeritus at Princeton University
The Science of Choosing the Appropriate Discount Rate
Discounted cash flow (DCF) analysis is one of the most commonly used valuation methods. In DCF models, the value of an asset is found by calculating the discounted present value of the asset’s future cash flows.
Our research shows DCF models can overstate the true value of a business or an asset. This is because traditional DCF analysis does not account for the risk that an asset’s or a business’s cash flows might not exist in the future. Even when cash-flow cessation risk is considered in a traditional DCF analysis, it is done so by making ad hoc adjustments to the discount rate. The basis for these adjustments is attributed to experience and expertise of the valuation expert. In two peer-reviewed journal studies, we develop a scientific method to incorporate cash-flow cessation risk within the DCF model’s discount rate without having to resort to any ad hoc adjustments. In this article, we summarize the two studies’ findings and provide a few illustrative examples.
Aside from the size of the cash flows, the most important input into a DCF analysis is the discount rate. Most investment texts recommend—and practitioners typically adopt— the weighted average cost of capital as the discount rate based on the Capital Asset Pricing Model (CAPM) framework. This cost of capital reflects the rate of return an investor would require to purchase an asset with a certain stream of cash flows. The CAPM framework assumes, however, the cash flows have an infinite life. While the cost of capital-based discount rate can provide a useful starting point, an adjustment to this rate is needed to arrive at a cessation risk-adjusted discount rate (RAD). Because RAD is higher than the cost of capital-based discount rate, the valuation of a business would be overstated in a typical DCF model. The extent of the overstatement, of course, will depend on the cash flow cessation risk, which is the risk that the business will cease to exist or fail in the future. This risk, in turn, depends on the nature of the business and the industry it is in.
Consider, for example, hedge funds. Many academic studies have shown that they have a relatively high rate of failure. There are numerous examples of large, established hedge funds suddenly failing or simply shuttering doors (e.g. Long-Term Capital Management, Tiger Management, Atticus Global, Amaranth). Many of the failed funds had a long and successful track record, suggesting that the risk of a fund’s failure does not recede with time. Our analysis of data from two widely-used hedge fund databases confirms that, in any given year, the average risk of a fund’s failure is around 7%.
An Illustrative Example: Valuing a Hedge Fund
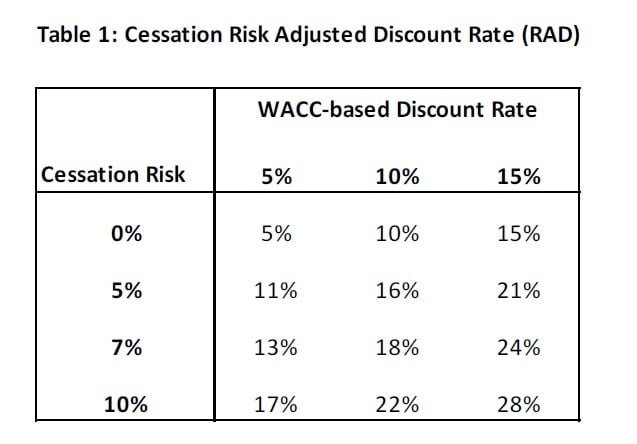
Suppose one were valuing a privately-held hedge fund. The first step would be to estimate the weighted average cost of capital (WACC) based on data on publicly-traded firms in the relevant segment of the financial sector. In Table 1, we compare the WACC-based discount rate to the risk-adjusted discount rate, (i.e., RAD); the difference between the two depends on the assumed failure rate, which is the cessation risk of the cash flows of the fund being valued. The details about the actual method of arriving at the RAD is contained in the journal articles, referenced at the end of this article.
In the first row of Table 1, where the cessation risk is zero, the RAD is the same as the WACC rate. However, that is not the case with a non-zero risk of cessation. For example, if the assumed cessation risk is 7% (consistent with the average failure rate of hedge funds), then the WACC-based discount rate of 5% translates to a RAD of 13%, more than two and a half times as large.
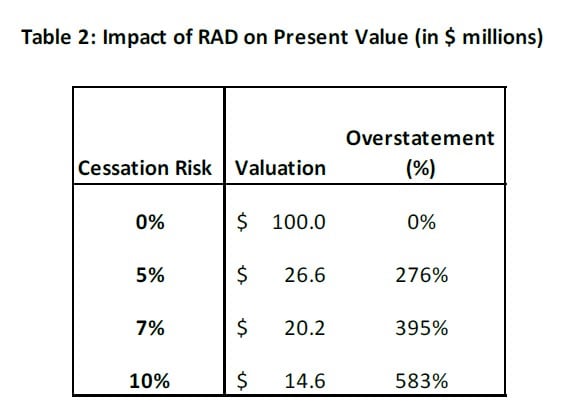
Next, we illustrate the impact of RAD on valuation. For ease of exposition, suppose the present value of the future cash flows of the hedge-fund is $100 million, assuming a WACC of 5% and no cessation risk. The figures in Table 2 illustrate the dramatic effect even a small risk of failure has on valuation. With an estimated failure or cessation risk of 7%, the valuation drops from $100 million to $20.2 million, assuming no residual/salvage value for the fund if it fails.3 In other words, a traditional DCF model, by not accounting for cessation risk, would overstate the value of the fund by nearly 400%!
Valuing Startups
One of the most common areas where practitioners intuitively factor cessation risk into discount rates is in startup valuation. It is widely known that venture capital firms, when valuing start-up businesses, often use a discount rate of 35% or higher, reflecting the risk the startup might fail.
The discount rates in the 35%-40% range in valuing startups are generally consistent with empirical data. For example, we find, for startup businesses, a failure rate of 12-15% is not uncommon. Consistent with the figures in Table 1, these failure rates would imply a RAD in the 35%-40% range.
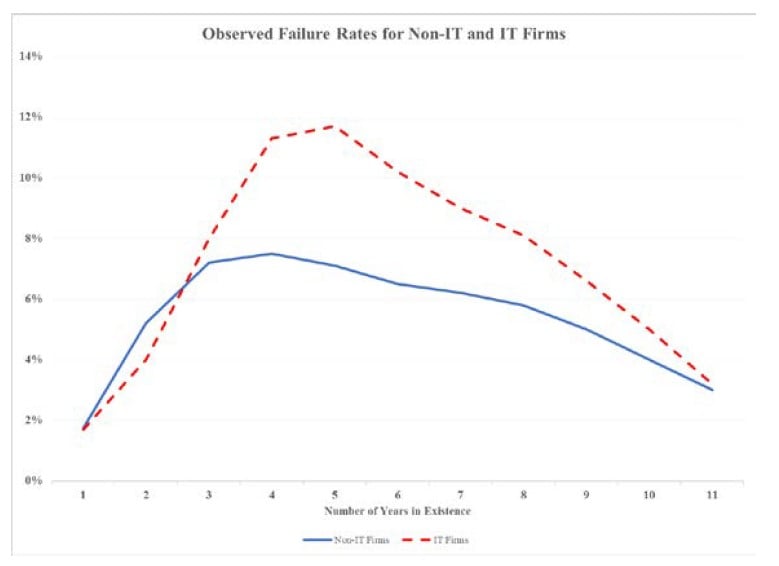
However, the failure rates of startups vary over time and by industry. In the chart below, we present data on failure rates of startups in the Information Technology (IT) and non-IT industries.
The chart shows the time-paths of failure rates have a distinct inverted-U shape: rising through the first four to five years of the firms’ existence, followed by a steady decline thereafter. Not unexpectedly, the failure rates of IT startups are higher.
Unlike in the case of hedge funds, it would thus be inappropriate to assume a constant i.e., time-invariant failure rate in valuing startup businesses. This implies the cessation risk-adjusted discount rate should be time-varying as well: rising in the first few years and then declining after that.
The two studies referenced here lay out a method to empirically test whether the assumption of time-varying cessation risk is appropriate and to estimate such risk over time. The studies also discuss a generalized approach to incorporate time-varying RADs in DCF models.
Concluding Comments
There are numerous valuation settings in which one cannot ignore the risk of the cash flows of the asset being valued would cease to exist. As illustrated in this article and more fully discussed in the studies referenced below, this risk of cessation can be incorporated into a standard DCF analysis. In fact, not accounting for the cessation risk can significantly overstate the valuation estimates in cases where such risk is material. One should, however, carefully consider whether and how one accounts for this risk based on the specific facts of any particular valuation assignment.
Article by Atanu Saha1 and Professor Burton Malkiel2
Referenced Research:
“DCF Valuation with Cash Flow Cessation Risk”
“Valuation of Cash Flows with Time-Varying Cessation Risk”
1 Chairman, Data Science Partners
2 The Chemical Bank Chairman’s Professor of Economics, Emeritus at Princeton University
3We are assuming here that there is no residual value left when the fund shuts down. In instances where there is diminution in value, rather than a total loss, appropriate adjustments should be made to our model in the calculation of terminal value. Our studies referenced in this article discusses these adjustments.