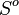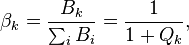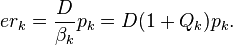For a more detailed discussion of this formula for the general case, see http://www.bjmath.com/bjmath/thorp/ch2.pdf.
Reasons to bet less than Kelly
A natural assumption is that taking more risk increases the probability of both very good and very bad outcomes. One of the most important ideas in Kelly is that betting more than the Kelly amount decreases the probability of very good results, while still increasing the probability of very bad results. Since in reality we seldom know the precise probabilities and payoffs, and since overbetting is worse than underbetting, it makes sense to err on the side of caution and bet less than the Kelly amount.
Kelly assumes sequential bets that are independent (later work generalizes to bets that have sufficient independence). That may be a good model for some gambling games, but generally does not apply in investing and other forms of risk-taking.
The Kelly property appears “in the long run” (that is, it is an asymptotic property). To a person, it matters whether the property emerges over a small number or a large number of bets. It makes sense to consider not just the long run, but where losing a bet might leave one in the short and medium term as well. A related point is that Kelly assumes the only important thing is long-term wealth. Most people also care about the path to get there. Kelly betting leads to highly volatile short-term outcomes which many people find unpleasant, even if they believe they will do well in the end.
The criterion assumes you know the true value of p, the probability of the winning. The formula tells you to bet a positive amount if p is greater than 1/(b+1). In many situations you cannot be sure p is the true probability. For example if you are told there are just 100 tickets ($1 each) to a raffle, and the prize for winning is $110, then Kelly will tell you to bet a positive fraction of your bank. However, if the information of “100 tickets” was a lie or mis-estimate, and if the true number of tickets was 120, then any bet needs to be avoided. Your optimal investement strategy will need to consider the statistical distribution for your estimate for p.
Bernoulli
In a 1738 article, Daniel Bernoulli suggested that when one has a choice of bets or investments that one should choose that with the highest geometric mean of outcomes. This is mathematically equivalent to the Kelly criterion[citation needed], although the motivation is entirely different (Bernoulli wanted to resolve the St. Petersburg paradox). The Bernoulli article was not translated into English until 1956,[12] but the work was well-known among mathematicians and economists.
Many horses[edit]
Kelly’s criterion may be generalized [13] on gambling on many mutually exclusive outcomes, like in horse races. Suppose there are several mutually exclusive outcomes. The probability that the k-th horse wins the race is 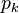

where 

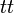
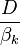
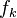
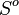
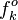
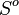
Step 1 Calculate the expected revenue rate for all possible (or only for several of the most promising) outcomes:
Step 2 Reorder the outcomes so that the new sequence 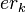
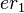
Step 3 Set 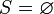
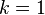


Step 4 Repeat:
If 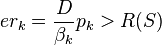


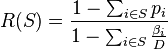
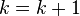
Else set 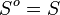
If the optimal set