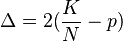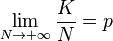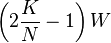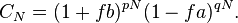Note that this reduces to the original expression for the special case above (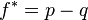
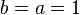
Clearly, in order to decide in favor of investing at least a small amount 
which obviously is nothing more than the fact that your expected profit must exceed the expected loss for the investment to make any sense.
The general result clarifies why leveraging (taking a loan to invest) decreases the optimal fraction to be invested , as in that case 


Proof
Heuristic proofs of the Kelly criterion are straightforward.[10] For a symbolic verification with Python and SymPy one would set the derivative y’(x) of the expected value of the logarithmic bankroll y(x) to 0 and solve for x:
>>> from sympy import *
>>> x,b,p = symbols('xbp')
>>> y = p*log(1+b*x) + (1-p)*log(1-x)
>>> solve(diff(y,x), x)
[-(1 - p - b*p)/b]
For a rigorous and general proof, see Kelly’s original paper[1] or some of the other references listed below. Some corrections have been published.[11]
We give the following non-rigorous argument for the case b = 1 (a 50:50 “even money” bet) to show the general idea and provide some insights.[1]
When b = 1, the Kelly bettor bets 2p – 1 times initial wealth, W, as shown above. If he wins, he has 2pW. If he loses, he has 2(1 – p)W. Suppose he makes N bets like this, and wins K of them. The order of the wins and losses doesn’t matter, he will have:
Suppose another bettor bets a different amount, (2p – 1 + 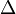
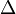
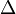
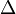
Take the derivative of this with respect to 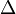
The turning point of the original function occurs when this derivative equals zero, which occurs at:
which implies:
but:
so in the long run, final wealth is maximized by setting 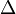
This illustrates that Kelly has both a deterministic and a stochastic component. If one knows K and N and wishes to pick a constant fraction of wealth to bet each time (otherwise one could cheat and, for example, bet zero after the Kth win knowing that the rest of the bets will lose), one will end up with the most money if one bets:
each time. This is true whether N is small or large. The “long run” part of Kelly is necessary because K is not known in advance, just that as N gets large, K will approach pN. Someone who bets more than Kelly can do better if K > pN for a stretch; someone who bets less than Kelly can do better if K < pN for a stretch, but in the long run, Kelly always wins.
The heuristic proof for the general case proceeds as follows.[citation needed]
In a single trial, if you invest the fraction 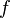
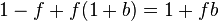
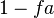
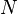
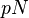

Maximizing 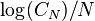

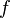


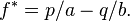
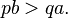

![(2p+Delta)^K[2(1-p)-Delta]^{N-K}W !](http://upload.wikimedia.org/math/a/4/b/a4b814d5ba30df6404506489e5905d33.png)
![K(2p+Delta)^{K-1}[2(1-p)-Delta]^{N-K}W-(N-K)(2p+Delta)^K[2(1-p)-Delta]^{N-K-1}W!](http://upload.wikimedia.org/math/1/2/f/12f40e12d0632addfa09de7b4509b3c7.png)
![K[2(1-p)-Delta]=(N-K)(2p+Delta) !](http://upload.wikimedia.org/math/d/3/8/d386e009e6ba02a60a46a9d992e43c64.png)